| Definitions | s = t, t  T, x:A T, x:A  B(x), B(x),  x:A. B(x), ES, a:A fp x:A. B(x), ES, a:A fp B(a), x:A B(a), x:A  B(x), Type, EqDecider(T), Unit, left + right, IdLnk, Id, EOrderAxioms(E; pred?; info), f(a), EState(T), Knd, B(x), Type, EqDecider(T), Unit, left + right, IdLnk, Id, EOrderAxioms(E; pred?; info), f(a), EState(T), Knd,   x. t(x), x. t(x),   x,y. t(x;y), kindcase(k; a.f(a); l,t.g(l;t) ), Msg(M), type List, x,y. t(x;y), kindcase(k; a.f(a); l,t.g(l;t) ), Msg(M), type List,  , , 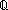 , val-axiom(E;V;M;info;pred?;init;Trans;Choose;Send;val;time), e < e', r , val-axiom(E;V;M;info;pred?;init;Trans;Choose;Send;val;time), e < e', r  s, P s, P   Q, Q,  , ,  b, constant_function(f;A;B), Top, strong-subtype(A;B), AbsInterface(A), let x,y = A in B(x;y), b, constant_function(f;A;B), Top, strong-subtype(A;B), AbsInterface(A), let x,y = A in B(x;y),  , Dec(P), x(s), P , Dec(P), x(s), P   Q, P Q, P    Q, E, P Q, E, P  Q, Q,  A, e A, e   X, A c X, A c B, t.1, case b of inl(x) => s(x) | inr(y) => t(y), if b then t else f fi , {x:A| B(x)} , ff, inr x , tt, inl x , True, B, t.1, case b of inl(x) => s(x) | inr(y) => t(y), if b then t else f fi , {x:A| B(x)} , ff, inr x , tt, inl x , True,  x.A(x), Void, x.A(x), Void, 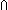 x:A.B(x), f x:A.B(x), f  g, f(x)?z, loc(e), vartype(i;x), state@i, State(ds), State(ds), <a, b>, x g, f(x)?z, loc(e), vartype(i;x), state@i, State(ds), State(ds), <a, b>, x  dom(f), False, {T}, S dom(f), False, {T}, S  T, suptype(S; T), g glues Ia:Qa T, suptype(S; T), g glues Ia:Qa   f f  Ib:Rb, f o g, [P? f : g], Ib:Rb, f o g, [P? f : g],  x:A. B(x), Q x:A. B(x), Q 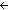 ==f== P, Inj(A;B;f), f is Q-R-pre-preserving on P, Q ==f== P, Inj(A;B;f), f is Q-R-pre-preserving on P, Q 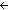 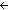 = f== P, {I}, X(e), (x = f== P, {I}, X(e), (x  l), l),  T, b | a, a ~ b, a T, b | a, a ~ b, a  b, a <p b, a < b, x f y, b, a <p b, a < b, x f y,  x x L. P(x), ( L. P(x), ( x x L.P(x)), r < s, q-rel(r;x), Outcome, l_disjoint(T;l1;l2), (e <loc e'), e L.P(x)), r < s, q-rel(r;x), Outcome, l_disjoint(T;l1;l2), (e <loc e'), e  loc e' , (e < e'), e c loc e' , (e < e'), e c e', e',  e<e'.P(e), e<e'.P(e),  e e e'.P(e), e'.P(e),  e<e'. P(e), e<e'. P(e),  e e e'.P(e), e'.P(e),  e e [e1,e2).P(e), [e1,e2).P(e),  e e [e1,e2).P(e), [e1,e2).P(e),  e e [e1,e2].P(e), [e1,e2].P(e),  e e [e1,e2].P(e), [e1,e2].P(e),  e e (e1,e2].P(e), SqStable(P), a =!x:T. Q(x), InvFuns(A;B;f;g), IsEqFun(T;eq), Refl(T;x,y.E(x;y)), Sym(T;x,y.E(x;y)), Trans(T;x,y.E(x;y)), AntiSym(T;x,y.R(x;y)), Connex(T;x,y.R(x;y)), CoPrime(a,b), Ident(T;op;id), Assoc(T;op), Comm(T;op), Inverse(T;op;id;inv), BiLinear(T;pl;tm), IsBilinear(A;B;C;+a;+b;+c;f), IsAction(A;x;e;S;f), Dist1op2opLR(A;1op;2op), fun_thru_1op(A;B;opa;opb;f), FunThru2op(A;B;opa;opb;f), Cancel(T;S;op), monot(T;x,y.R(x;y);f), IsMonoid(T;op;id), IsGroup(T;op;id;inv), IsMonHom{M1,M2}(f), a (e1,e2].P(e), SqStable(P), a =!x:T. Q(x), InvFuns(A;B;f;g), IsEqFun(T;eq), Refl(T;x,y.E(x;y)), Sym(T;x,y.E(x;y)), Trans(T;x,y.E(x;y)), AntiSym(T;x,y.R(x;y)), Connex(T;x,y.R(x;y)), CoPrime(a,b), Ident(T;op;id), Assoc(T;op), Comm(T;op), Inverse(T;op;id;inv), BiLinear(T;pl;tm), IsBilinear(A;B;C;+a;+b;+c;f), IsAction(A;x;e;S;f), Dist1op2opLR(A;1op;2op), fun_thru_1op(A;B;opa;opb;f), FunThru2op(A;B;opa;opb;f), Cancel(T;S;op), monot(T;x,y.R(x;y);f), IsMonoid(T;op;id), IsGroup(T;op;id;inv), IsMonHom{M1,M2}(f), a  b, IsIntegDom(r), IsPrimeIdeal(R;P), loc(e), kind(e), SWellFounded(R(x;y)), pred!(e;e'), first(e), pred(e), E(X), (I| b, IsIntegDom(r), IsPrimeIdeal(R;P), loc(e), kind(e), SWellFounded(R(x;y)), pred!(e;e'), first(e), pred(e), E(X), (I| p), P & Q, (I|p), X p), P & Q, (I|p), X 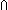 Y = 0, [f?g], R|P, R1 Y = 0, [f?g], R|P, R1  R2, R1 R2, R1    R2, bool-decider(b), |g|, MonHom(M1,M2), p-filter(f), do-apply(f;x), if p:P then A(p) else B fi , t ...$L, SQType(T), s ~ t R2, bool-decider(b), |g|, MonHom(M1,M2), p-filter(f), do-apply(f;x), if p:P then A(p) else B fi , t ...$L, SQType(T), s ~ t |